346gr. Τυχαίες μεταβλητές, πυκνότητες πιθανότητας, κατανομές

Πληροφοριακά Στοιχεία: Γράφτηκε από τον/την Χατζηλιόντος Χριστόδουλος; Δημοσιεύθηκε : 04 Νοέμβριος 2020; Δημιουργήθηκε : 04 Νοέμβριος 2020; Τελευταία ενημέρωση : 09 Νοέμβριος 2020

Αξιολόγηση Χρήστη: 5 / 5

Τυχαίες μεταβλητές, πυκνότητες πιθανότητας, κατανομές.

Κατανομή Bernoulli

Πυκνότητα	Πιθανότητα	Μέση	Διακύμανση
		p	p q
Διάγραμμα πυκνότητας

Διάγραμμα πιθανότητας

Για την τυχαία μεταβλητή Χ με πεδίο τιμών την τιμή 0 με πιθανότητα q=1-p και την τιμή 1 με πιθανότητα p, η Χ ακολουθεί την Κατανομή Bernoulli.

Διωνυμική κατανομή

Πυκνότητα	Πιθανότητα	Μέση	Διακύμανση
		n p	n p q
Διάγραμμα πυκνότητας

Διάγραμμα πιθανότητας

Αν X είναι ο αριθμός των επιτυχιών σε μια ακολουθία n δοκιμών Bernoulli, τότε η X ακολουθεί την διωνυμική κατανομή b(x;n,p).
Για την ακολoυθία ανεξάρτητων τυχαίων μεταβλητών Bernoulli, X₁ ,X₂ ,..., X_n με παράμετρο p, η τυχαία μεταβλητή X = X₁ + X₂ +...+ X_n ακολουθεί την διωνυμική κατανομή b(x;n,p).

Αρνητική διωνυμική κατανομή - Κατανομή Pascal

Πυκνότητα	Πιθανότητα	Μέση	Διακύμανση

Διάγραμμα πυκνότητας

Διάγραμμα πιθανότητας

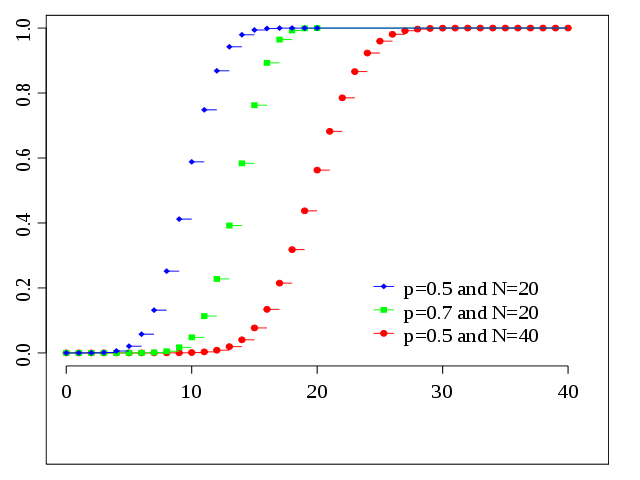
Αν X είναι ο αριθμός των αποτυχιών σε μια ακολουθία δοκιμών Bernoulli, μέχρι να εμφανιστούν r επιτυχίες, τότε η X ακολουθεί την κατανομή Pascal NB(x;r,p).
Για την ακολoυθία ανεξάρτητων τυχαίων μεταβλητών, της γεωμετρικής κατανομής, X₁ ,X₂ ,..., X_n με παράμετρο p, η τυχαία μεταβλητή X = X₁ + X₂ +...+ X_n ακολουθεί την κατανομή Pascal NB(x;r,p).

Γεωμετρική κατανομή

Πυκνότητα	Πιθανότητα	Μέση	Διακύμανση

Διάγραμμα πυκνότητας

Διάγραμμα πιθανότητας

Για την διακριτή τυχαία μεταβλητή Χ, που αποτελεί τον αριθμό των αποτυχιών, με πιθανότητα 1-p, σε μια σειρά δοκιμών Bernoulli, πριν εμφανιστεί η πρώτη επιτυχία, η Χ ακολουθεί την γεωμετρική κατανομή G(x;p).

Υπεργεωμετρική κατανομή

Πυκνότητα	Πιθανότητα	Μέση	Διακύμανση

Διάγραμμα πυκνότητας

Διάγραμμα πιθανότητας

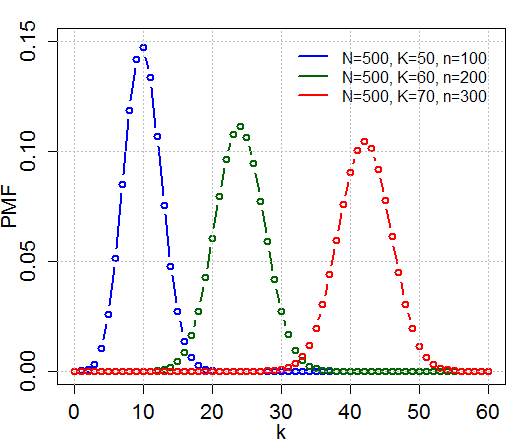
Η διακριτή τυχαία μεταβλητή Χ αυτής της παραγράφου, με n=1, 2, ..., N=1, 2, ..., m= 0, 1, 2, ...,N, x=0, 1, 2, ..., min(m,n), ακολουθεί την υπεργεωμετρική κατανομή h(x;N,n,m).
Η διακριτή τυχαία μεταβλητή Χ της υπεργεωμετρικής κατανομής, με σταθερό x, n και p=m/N και για πολύ μεγάλο Ν, ακολουθεί ασυμπτωτικά την διωνυμική κατανομή b(x;n,p).

Κατανομή Poisson

Πυκνότητα	Πιθανότητα	Μέση	Διακύμανση
${\frac {\lambda ^{k}e^{-\lambda }}{k!}}$	ή	λ	λ
Διάγραμμα πυκνότητας

Διάγραμμα πιθανότητας

Αν X είναι ο αριθμός των επιτυχιών σε μια ακολουθία n δοκιμών Bernoulli, με n πολύ μεγάλο, p πολύ μικρό και σταθερό γινόμενο λ = n p, τότε η X ακολουθεί ασυμπτωτικά την κατανομή Poisson P(x;n,p).

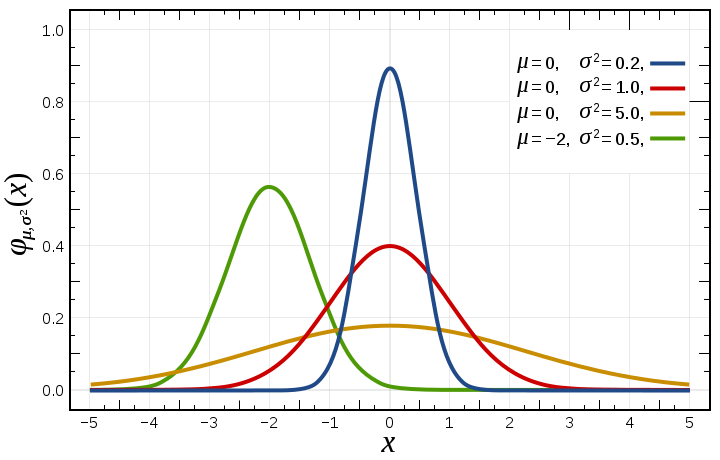
Κανονική κατανομή

Πυκνότητα	Πιθανότητα	Μέση	Διακύμανση
$f(x)={\tfrac {1}{\sqrt {2\pi \sigma ^{2}}}}\,e^{-(x-\mu )^{2}/2\sigma ^{2}}$	${\frac {1}{2}}\left[1+\operatorname {erf} \left({\frac {x-\mu }{\sigma {\sqrt {2}}}}\right)\right]$	μ	σ²
Διάγραμμα πυκνότητας

Διάγραμμα πιθανότητας

Για την τυχαία μεταβλητή Χ, που ακολουθεί την κανονική κατανομή 𝛮(𝜇, 𝜎²), η τυχαία μεταβλητή 𝛶 = (𝛸−𝜇)/𝜎 ακολουθεί την κανονική κατανομή 𝛮(0, 1).
Για τις 𝑋₁ και 𝑋₂ ανεξάρτητες τυχαίες μεταβλητές, που ακoλουθούν τις κανονικές κατανομές 𝛮(𝜇₁, 𝜎₁²) και 𝛮(𝜇₂, 𝜎₂²), αντίστοιχα, η τυχαία μεταβλητή 𝛧 = 𝑋₁ ± 𝑋₂ ακολουθεί την κανονική κατανομή 𝛮(𝜇₁ ± 𝜇₂, 𝜎₁² + 𝜎₂²).
Για το τυχαίο δείγμα X = (𝛸₁, 𝛸₂, … , 𝛸_𝑛), από κανονική κατανομή 𝛮(𝜇, 𝜎²), η δειγματική μέση τιμή (δμτ) 𝛸 ακολουθεί την κανονική κατανομή 𝛮(𝜇, 𝜎²/n).
Για το τυχαίο δείγμα X = (𝛸₁, 𝛸₂, … , 𝛸_𝑛), από κατανομή Fischer 𝐹(𝑥), για την οποία ισχύει ότι 𝐸(𝑋_𝑖) = 𝜇 και Var(𝑋_𝑖) = 𝜎² < ∞, η τυχαία μεταβλητή (𝛸−𝜇) / (𝜎/√𝑛) συγκλίνει κατά νόμο στην τυπική κανονική κατανομή, που σημαίνει ότι, για αρκούντος μεγάλο 𝑛 ( 𝑛 ≥ 30 ), ακολουθεί την τυπική κανονική κατανομή 𝛮(0,1).
Για τα ανεξάρτητα τυχαία δείγματα X = (𝛸₁, 𝛸₂, … , 𝛸_𝑛) και Y = (Y₁, Y₂, … , Y_m), από κανονική κατανομή 𝛮(𝜇₁, 𝜎₁²) και 𝛮(𝜇₂, 𝜎₂²), αντίστοιχα, η τυχαία μεταβλητή (δμτ 𝑋 − δμτ 𝑌) ακολουθεί την κανονική κατανομή 𝛮(𝜇 = 𝜇₁ − 𝜇₂, 𝜎²= (𝜎₁²/n) + (𝜎₂²/m) ).

Κατανομή Student

Πυκνότητα	Πιθανότητα	Μέση	Διακύμανση
		0
Διάγραμμα πυκνότητας

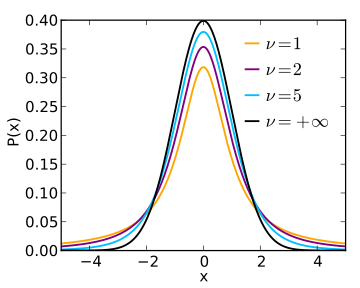Διάγραμμα πιθανότητας

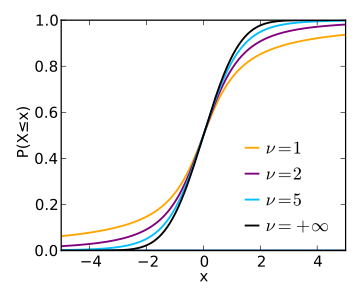Για τις ανεξάρτητες τυχαίες μεταβλητές 𝑋₁ και 𝑋₂, όπου 𝑋₁ ακολουθεί την κανονική κατανομή 𝛮(0,1) και η 𝑋₂ ακoλουθεί την κατανομή Chi Square 𝓧_𝑛², η τυχαία μεταβλητή 𝑌 = 𝑋₁ / √(𝑋₂/𝑛) ακολουθεί την κατανομή Student 𝑡_𝑛.
Για το τυχαίο δείγμα X = (𝛸₁, 𝛸₂, … , 𝛸_𝑛), από την κανονική κατανομή 𝛮(𝜇, 𝜎²), οι τυχαίες μεταβλητές δμτ 𝛸 και 𝑆² είναι ανεξάρτητες και η τυχαία μεταβλητή (δμτ 𝛸−𝜇) / (𝜎/√𝑛) ακολουθεί την κατανομή Student 𝑡_𝑛-1.
Για τα ανεξάρτητα τυχαία δείγματα X = (𝛸₁, 𝛸₂, … , 𝛸_𝑛) και Y = (Y₁, Y₂, … , Y_m), από κανονική κατανομή 𝛮(𝜇₁, 𝜎₁²) και 𝛮(𝜇₂, 𝜎₂²), με δειγματική μέση τιμή X και Y, με δειγματική διασπορά 𝑆₁² και 𝑆₂², αντίστοιχα, η [(δμτ Χ - δμτ Υ) - (μ₁ - μ₂)] / S, όπου S = √[(n-1)S₁²+(m-1)S₂²] √[n+m] / √[n+m-2] √[nm] , ακολουθεί την κατανομή Student 𝑡_𝑛+m-2.

Κατανομή Fischer

Πυκνότητα	Πιθανότητα	Μέση	Διακύμανση

Διάγραμμα πυκνότητας

Διάγραμμα πιθανότητας

Για τις ανεξάρτητες τυχαίες μεταβλητές 𝛸₁ και 𝛸₂, που ακολουθούν τις κατανομές Chi Square 𝓧²_𝑛1 και 𝓧²_𝑛2, αντίστοιχα, η τυχαία μεταβλητή 𝑌 = (𝑋₁/𝑛₁) / (𝑋₂/𝑛₂) ακολουθεί την κατανομή Fischer 𝐹(𝑛₁, 𝑛₂).
Για τα ανεξάρτητα τυχαία δείγματα X = (𝛸₁, 𝛸₂, … , 𝛸_𝑛) και Y = (Y₁, Y₂, … , Y_m), από κανονική κατανομή 𝛮(𝜇₁, 𝜎₁²) και 𝛮(𝜇₂, 𝜎₂²), με δειγματική διασπορά 𝑆₁² και 𝑆₂², αντίστοιχα, η (𝑆₁²/𝜎₁²) ⁄ (𝑆₂²/𝜎₂²) ακολουθεί την κατανομή Fischer 𝐹(𝑛−1, 𝑚 −1).

Κατανομή Chi Square

Πυκνότητα	Πιθανότητα	Μέση	Διακύμανση
		k	2k
Διάγραμμα πυκνότητας

Διάγραμμα πιθανότητας

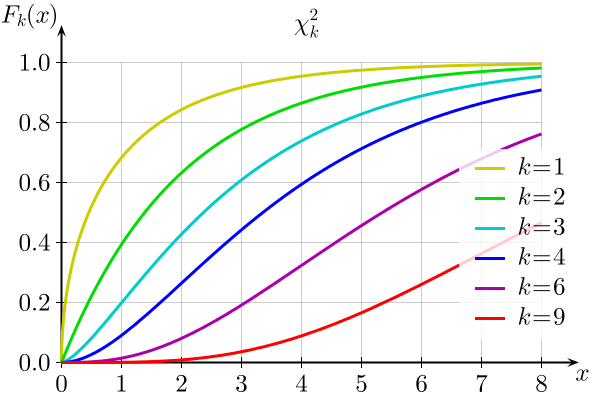Για τις ανεξάρτητες τυχαίες μεταβλητές 𝛸₁, 𝛸₂, … , 𝛸_𝑛, που ακολουθούν την κανονική κατανομή 𝛮(0,1), η καθεμία, η τυχαία μεταβλητή 𝑌 = ∑ 𝑋_𝑖² ακολουθεί την κατανομή Chi Square 𝓧²_𝑛.
Για τις ανεξάρτητες τυχαίες μεταβλητές 𝛸₁, 𝛸₂, … , 𝛸_𝑘, που ακολουθούν τις κατανομές Chi Square 𝓧²_𝑛𝑖, 𝑖 = 1,2, … , 𝑘, αντίστοιχα, η τυχαία μεταβλητή 𝑌 = ∑ 𝑋²_𝑖 ακολουθεί την κατανομή Chi Square 𝓧²_𝑛, όπου 𝑛 = 𝑛₁ + 𝑛₂ + ⋯ + 𝑛_𝑘 .
Για τις ανεξάρτητες τυχαίες μεταβλητές 𝛸₁ και 𝛸₂, που ακoλουθούν η 𝑋₁ την κατανομή Chi Square 𝓧²_𝑛1 και η 𝑋₁ + 𝑋₂ την κατανομή Chi Square 𝓧²_𝑛, με 𝑛 > 𝑛₁, η 𝑋₂ ακολουθεί την κατανομή Chi Square 𝓧²_𝑛−𝑛1 .
Για το τυχαίο δείγμα X = (𝛸₁, 𝛸₂, … , 𝛸_𝑛), από την κανονική κατανομή 𝛮(𝜇, 𝜎²), οι τυχαίες μεταβλητές δμτ 𝛸 και 𝑆² είναι ανεξάρτητες και η τυχαία μεταβλητή (𝑛−1) 𝑆² / 𝜎² ακολουθεί την κατανομή Chi Square 𝓧²_𝑛−1.

Διάβασε επίσης:

Η Kemioteko Engineering δημιουργήθηκε ως απόσταγμα εμπειριών 14 ετών στην αδειοδότηση, κατασκευή και λειτουργία δημόσιων τεχνικών έργων και 8 ετών στο ελεύθερο επάγγελμα του μελετητή μηχανικού με εξειδίκευση στην αδειοδότηση και λειτουργία επιχειρήσεων. Αποστολή της Kemioteko Engineering - Χατζηλιόντος Ι. Χριστόδουλος είναι η δημιουργία πελατών, οπαδών της, βαθειά ικανοποιημένων, που θέλουν να κάνουν διαχρονικά τα σωστά πράγματα με τους κατάλληλους συνεργάτες.

Διπλ. Χημικός Μηχανικός ΕΜΠ - Msc Περιβαλλοντικού Σχεδιασμού

Αγρονόμος Τοπογράφος Μηχανικός ΑΠΘ - 5ο Εξάμηνο

Επιθεωρητής Ξενοδοχείων - ΕΕΔΔ - TUV Austria RCN 6035/2016

Επιθεωρητής ISO 9001 - TUV Austria RCN 6065/2016

Επιθεωρητής ISO 45001 - Alison 1412-13849119

Επιθεωρητής GDPR - Alison 1401-13849119

Ενεργειακός Επιθεωρητής - No 16109 | No 553

Μελετητής ΥΠΕΧΩΔΕ - No 26837 - 18-A & 27-A

ΑΜ ΤΕΕ - No 83488 | ΤΕΧΝΙΚΟΣ ΑΣΦΑΛΕΙΑΣ. 330512/2017
Μητρώο Αξιολογητών ΓΓΕΤ- No 14856/95711/08-06-17

Ελεγκτής Δόμησης - No 4517

τηλ +302399-022359

Βασ Πιτσούλη 1, TK 63080, Νέα Καλλικράτεια